A consistent measurement system for photography
Everybody who starts with photography must eventually come to grapple with f/numbers, shutter settings, focal lengths and ISO values. The problem with the current system is that they are all on different measurement systems. Focal length and ISO are linear, shutter speeds are expressed as fractions, and apertures are proportional to the square root of the amount of light.
The end result of these different scales is that the actual values are just about useless for any practical calculation a photographer might need to do.
For example let's say that you are wondering what ISO you will need to photograph a stationary object lit by streetlights, using a 28mm f/2.8 on a full frame DSLR. Street lighting is usually around 15 lux, which is about LV 2. LV 0 is defined as the amount of light that requires 1 second exposure at f/1 and ISO 100, and LV 2 is two stops brighter than that. Let's see, f/2.8 is - f/1, f/1.4, f/2, f/2.8... Three stops darker than f/1. Three minus two is one, so we need one stop longer shutter speed than LV 0. So at f/2.8, we would need 2 seconds of exposure (one stop up from the one second of LV 0), which is too long to handhold with a 28mm lens.
According to the reciprocal rule, we would like to have an exposure time which is smaller than one divided by the focal length. For a 28mm lens, we would like to have at least 1/32s to handhold reliably, which is (count off again... 2s, 1s, 1/2, 1/4, 1/8, 1/16, 1/32) six stops darker than 2 seconds. What ISO is six stops more sensitive than ISO 100? Again, we count off: ISO 100, ISO 200, ISO 400, ISO 800, ISO 1600, ISO 3200, ISO 6400. So to handhold reliably under streetlights at 28mm f/2.8, you will need ISO 6400. That took counting off three times to get the value we needed. It's not that it's impossible, but the numbers themselves are essentially useless.
Of course pros and serious amateurs can do this sort of thing in their head, but the calculation would not have been significantly easier if f/stops were named Alpha, Beta, Gamma, Delta... ISOs were called A, B, C, D, and the shutter times were called Andrew, Bob, Charlie, and David. As long as we remember what order they are in, the numbers themselves are completely useless.
In fact they are downright misleading, in many cases. For example my D90 used to go to ISO 3200. My new D750 goes to ISO 12800. Wow, that's 9600 more ISO! That's a lot right? Not really: it's two more stops, same as from ISO 200 to ISO 800.
So what could this be replaced with? Introducing: the Harmonized Photography Scaling System.
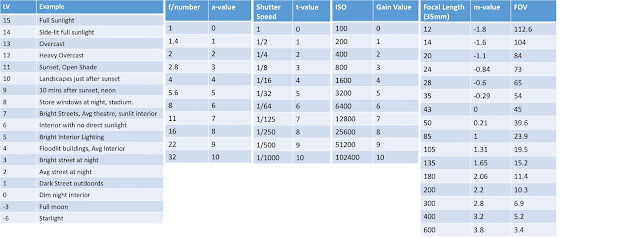
The idea of the scale is simple, I just transformed everything to stops. For aperture, time, and ISO that is straightforward, but I decided to do this for lenses as well. Therefore a normal lens is defined as 0, a lens twice the length of the normal is defined as 1, a lens four times the normal is defined as 2 etc. Notice that in this case I'm taking the high road and using 43mm as the length of the normal lens for the 35mm system. This is the actual diagonal of the 24x36mm frame, which is how normal lenses are generally defined. Oskar Barnack, the inventor of the Leica system, used 50mm just because he happened to have those lenses available, but in fact they are very short telephotos.
So let's look at our original problem, with the new scales. In this system, the equivalent of the reciprocal rule is the 6rule: you need a time value that is six stops larger than your magnification. The 28mm f/2.8 is now a -0.6m 3a (-0.6 magnification, aperture 3). So starting from -0.6m, we need at least 5.6t. To this we add 3a, to get 8.6. We need to hit LV 2, and 8.6-2 = 6.6. So we need a Gain of between six and seven, which is a little over ISO 6400, reassuringly equivalent to what we calculated the hard way before.
Let's look at some other questions. Is it easier to handhold a 24mm f/4 (-0.84m 4a), or a 85m f/1.4 (1m 1a)? Just by adding m and a, we can see that the 85mm can be handheld with almost two stops less ambient light (m+a= 3.84 vs 2).
I recently bought a Nikkor 28-300mm f/3.5-5.6 VR. How much light would I need to handhold it at the tele end (this is the question I was trying to answer when I formulated the system). In terms of the HPSS, the lens is called a Nikkor -0.6_2.8m 3.6_5a, so in principle we would need at least 2.8+5+6= LV 13.6 to shoot it at ISO 100, hand held. This is equivalent to a very light overcast, or side light in direct sunlight. But wait! The lens has VR, so we can probably get away with two stops less, or LV 11. This is the light level of open shade, or a landscape illuminated by sunset. And if we're shooting with a modern full frame DSLR, we shouldn't be worried about using gains as high as 5 (ISO 3200), which gets us get down to 11-5= LV 6. This is a daylight interior without direct sunlight, or the average level of light in a theater.
The system also allows you to calculate approximately how defocused the background will be. For example, let's say we want to photograph a 1m tall subject in portrait orientation, and we want to know whether a 85mm f/1.4 (1m 1a) or a 200mm f/2.8 (2.2m 3a) will throw the background more out of focus. Just subtract half the a-value from the magnification, and compare the two numbers. The 85mm gives us 0.5, while the 200mm gives 0.7. This tells us that the 200mm will have slightly more blurred background. You can confirm this is the case using the dofsimulator (the two lenses discussed are already set up as saved values).
I don't expect the major manufacturers to change the naming conventions for lenses any time soon, but if you memorize the relevant values for your lenses (or maybe tape them inside your lens cap?) , it will help you to perform calculations in the field. Also, converting the standard values to this system should prove useful when you are comparing lenses, to decide which ones to buy.
Hope this helps!
The end result of these different scales is that the actual values are just about useless for any practical calculation a photographer might need to do.
For example let's say that you are wondering what ISO you will need to photograph a stationary object lit by streetlights, using a 28mm f/2.8 on a full frame DSLR. Street lighting is usually around 15 lux, which is about LV 2. LV 0 is defined as the amount of light that requires 1 second exposure at f/1 and ISO 100, and LV 2 is two stops brighter than that. Let's see, f/2.8 is - f/1, f/1.4, f/2, f/2.8... Three stops darker than f/1. Three minus two is one, so we need one stop longer shutter speed than LV 0. So at f/2.8, we would need 2 seconds of exposure (one stop up from the one second of LV 0), which is too long to handhold with a 28mm lens.
According to the reciprocal rule, we would like to have an exposure time which is smaller than one divided by the focal length. For a 28mm lens, we would like to have at least 1/32s to handhold reliably, which is (count off again... 2s, 1s, 1/2, 1/4, 1/8, 1/16, 1/32) six stops darker than 2 seconds. What ISO is six stops more sensitive than ISO 100? Again, we count off: ISO 100, ISO 200, ISO 400, ISO 800, ISO 1600, ISO 3200, ISO 6400. So to handhold reliably under streetlights at 28mm f/2.8, you will need ISO 6400. That took counting off three times to get the value we needed. It's not that it's impossible, but the numbers themselves are essentially useless.
Of course pros and serious amateurs can do this sort of thing in their head, but the calculation would not have been significantly easier if f/stops were named Alpha, Beta, Gamma, Delta... ISOs were called A, B, C, D, and the shutter times were called Andrew, Bob, Charlie, and David. As long as we remember what order they are in, the numbers themselves are completely useless.
In fact they are downright misleading, in many cases. For example my D90 used to go to ISO 3200. My new D750 goes to ISO 12800. Wow, that's 9600 more ISO! That's a lot right? Not really: it's two more stops, same as from ISO 200 to ISO 800.
So what could this be replaced with? Introducing: the Harmonized Photography Scaling System.
So let's look at our original problem, with the new scales. In this system, the equivalent of the reciprocal rule is the 6rule: you need a time value that is six stops larger than your magnification. The 28mm f/2.8 is now a -0.6m 3a (-0.6 magnification, aperture 3). So starting from -0.6m, we need at least 5.6t. To this we add 3a, to get 8.6. We need to hit LV 2, and 8.6-2 = 6.6. So we need a Gain of between six and seven, which is a little over ISO 6400, reassuringly equivalent to what we calculated the hard way before.
Let's look at some other questions. Is it easier to handhold a 24mm f/4 (-0.84m 4a), or a 85m f/1.4 (1m 1a)? Just by adding m and a, we can see that the 85mm can be handheld with almost two stops less ambient light (m+a= 3.84 vs 2).
I recently bought a Nikkor 28-300mm f/3.5-5.6 VR. How much light would I need to handhold it at the tele end (this is the question I was trying to answer when I formulated the system). In terms of the HPSS, the lens is called a Nikkor -0.6_2.8m 3.6_5a, so in principle we would need at least 2.8+5+6= LV 13.6 to shoot it at ISO 100, hand held. This is equivalent to a very light overcast, or side light in direct sunlight. But wait! The lens has VR, so we can probably get away with two stops less, or LV 11. This is the light level of open shade, or a landscape illuminated by sunset. And if we're shooting with a modern full frame DSLR, we shouldn't be worried about using gains as high as 5 (ISO 3200), which gets us get down to 11-5= LV 6. This is a daylight interior without direct sunlight, or the average level of light in a theater.
The system also allows you to calculate approximately how defocused the background will be. For example, let's say we want to photograph a 1m tall subject in portrait orientation, and we want to know whether a 85mm f/1.4 (1m 1a) or a 200mm f/2.8 (2.2m 3a) will throw the background more out of focus. Just subtract half the a-value from the magnification, and compare the two numbers. The 85mm gives us 0.5, while the 200mm gives 0.7. This tells us that the 200mm will have slightly more blurred background. You can confirm this is the case using the dofsimulator (the two lenses discussed are already set up as saved values).
I don't expect the major manufacturers to change the naming conventions for lenses any time soon, but if you memorize the relevant values for your lenses (or maybe tape them inside your lens cap?) , it will help you to perform calculations in the field. Also, converting the standard values to this system should prove useful when you are comparing lenses, to decide which ones to buy.
Hope this helps!

Comments
Post a Comment